Resource	Info
Paper	http://arxiv.org/abs/2509.07558
Code & Data	https://github.com/zerolllin/Delta-L-Normalization
Public	arXiv
Date	2025.09.22

Summary Overview

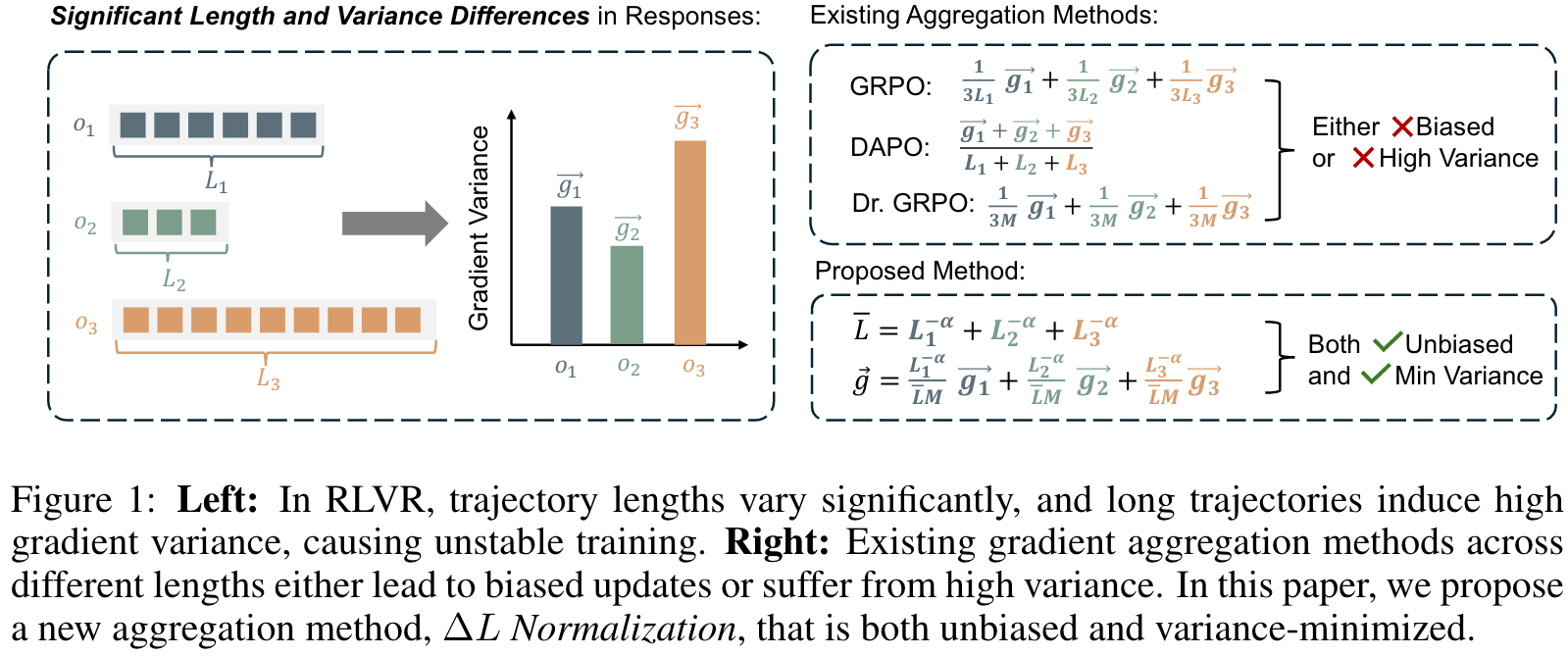
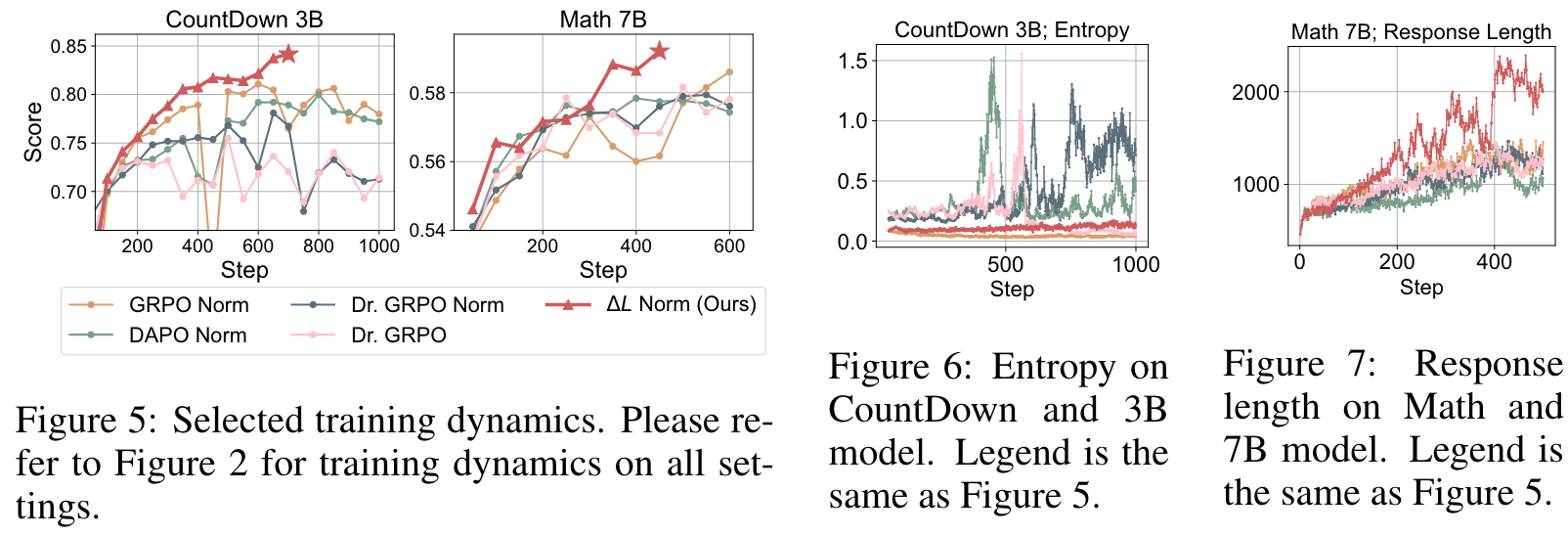
Although previous methods such as GRPO, DAPO, and Dr. GRPO introduce different loss normalization terms to address this issue, they either produce biased estimates or still suffer from high gradient variance. By analyzing the effect of varying lengths on policy loss both theoretically and empirically, we reformulate the problem as finding a minimum-variance unbiased estimator. Our proposed $\Delta L\;Normalization$ not only provides an unbiased estimate of the true policy loss but also minimizes gradient variance in theory.

Main Content

GRPO applies a sample-level normalization, dividing each sample-level loss by its response length; while DAPO uses a batch-level approach, normalizing the total loss by the sum of response lengths in the batch. In addition, because such length-dependent factors deviate from standard reinforcement learning theory. Dr. GRPO, in contrast, avoids any length-dependent factor and normalizes the gradient with a fixed constant.

There is a lack of analysis on how they influence the statistical properties of gradient estimation in RLVR, with gradient variance being particularly important because high variance leads to inefficient training and even model collapse.

(1) The aggregation startegies in GRPO and DAPO introduce length-dependent bias in estimating the true policy gradient. As response lengths increase, their parameter updates shrink in gradient norm, slowing convergence. (2) The aggregation strategies in DAPO and Dr. GRPO lead means greater relative noise for the same gradient norm, resulting in less stable training.

the variance of the unnormalized gradient $g_i$ grows approximately proportionally to the response length.

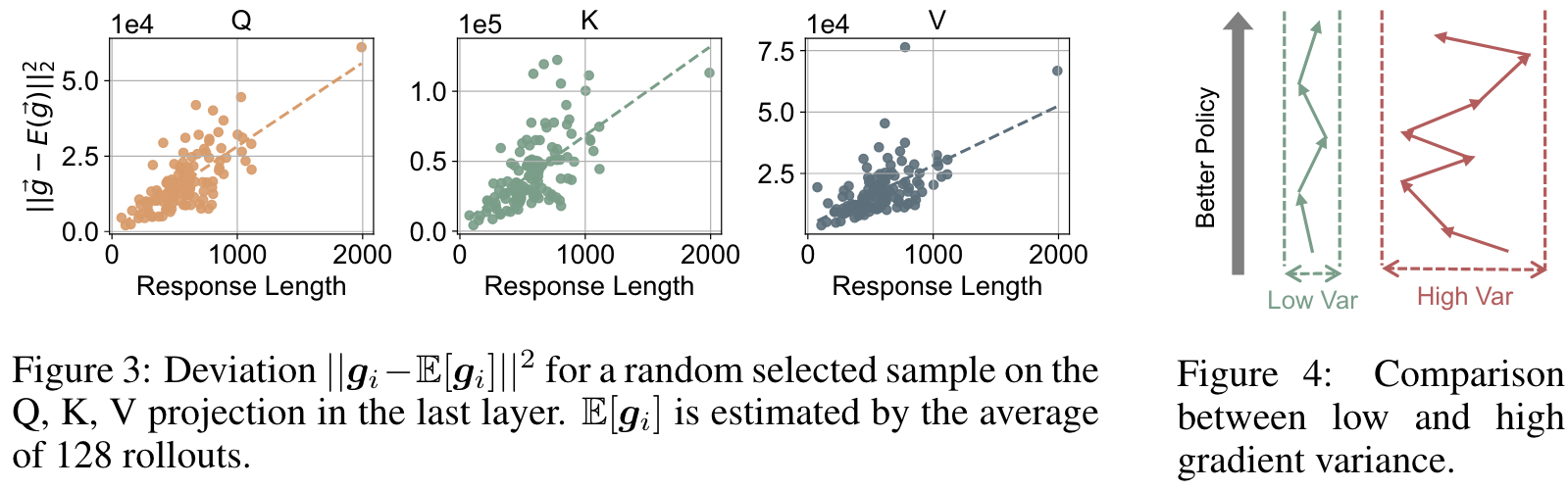
Consider $\text{Var}(g_i) \approx \text{Var}(\sum_{t=1}^{L_i} A_i \nabla_\theta \log \pi_\theta(o_{i,t} | q, o_{i,<t}))$. We approximate this as $\text{Var}(g_i) \approx \sum_{t=1}^{L_i} \text{Var}(A_i \nabla_\theta \log \pi_\theta(o_{i,t} | q, o_{i,<t}))$, by ignoring covariance between individual token-level gradients. Assuming each token-level term contributes approximately a constant variance $V$, we thus have $\text{Var}(g_i) \approx V \cdot L_i$. This approximation indicates that samples with longer responses inherently exhibit higher gradient variance due to increased randomness, and the gradient variance grows proportionally with response length.

GRPO and DAPO introduce length-dependent coefficients determined by the response lengths $L_i$, which results in a $bias$ issue.

Rethink loss normalization in RLVR

Existing aggregation methods introduce either bias or excessive variance. We therefore ask: $Can a loss aggregation method be both unbiased and minimum-variance?$ The answer is yes. We observe that this problem can be naturally reformulated within the framework of minimum variance unbiased estimation in statistics. Specifically, we treat the gradients obtained from responses of different lengths as independent observations of the same underlying variable (the ground-truth policy gradient), each with its own variance. Our objective is then to construct a new unbiased estimator by optimally combining these observations so that the resulting variance is minimized. Formally, we define the problem as follows.

Problem Definition. Given a set of independent sample-level gradient estimators $\{g_i\}_{i=1}^G$ satisfying $\mathbb{E}[g_i] = \nabla_\theta J(\theta)$ and $\text{Var}(g_i) = V L_i$, where $L_i > 0$ denotes the length associated with sample $i$ and $V$ is a constant scalar, the objective is to determine coefficients $\{x_i\}_{i=1}^G$ in the linear combination $\hat{g} = \sum_{i=1}^G x_i g_i$, such that $\mathbb{E}[\hat{g}] = \nabla_\theta J(\theta) / M$ for a given $M > 0$, while minimizing the variance $\text{Var}[\hat{g}]$.

Noting that the unbiasedness constraint $\mathbb{E}[\hat{g}] = \nabla_\theta J(\theta) / M$ is equivalent to $\sum_{i=1}^G x_i = \frac{1}{M}$ and, by independence, the variance satisfies $\text{Var}[\hat{g}] = \sum_{i=1}^G x_i^2 \text{Var}(g_i) = V \sum_{i=1}^G L_i x_i^2$, the problem reduces to a convex quadratic program with a single linear constraint. Solving with the Lagrange multiplier method yields the unique minimizer: $x_i^* = \frac{1}{M} \frac{L_i^{-1}}{\sum_{j=1}^G L_j^{-1}}, \quad i = 1, \ldots, G$.

In practice, we find it is beneficial to introduce a hyperparameter $0 \leq \alpha \leq 1$ to the normalization factor, which gives the following normalization weights:

The parameter $\alpha$ provides a tradeoff between variance reduction and utilization of long responses. While longer responses tend to introduce higher variance, sometimes they also carry richer learning signals. Choosing $\alpha<1$ allows these signals to contribute more effectively, at the cost of increased gradient variance. We name this method $\Delta L\;Normalization$ , as it is specially designed to match the dynamic length nature in RLVR. It has four key properites:

• Unbiasedness: For any $\alpha$, $\Delta L\;Normalization$ is unbiased since $\sum_{i=1}^Gx_i=\frac{1}{M}$, ensuring $\mathbb{E}[\hat{g}]=\nabla_{\theta}J(\theta)/M$. This preserves theoretical consistency with vanilla reinforcement learning.
• Minimum Variance: Choosing $\alpha=1$ achieves the minimum possible variance under the unbiasedness constraint. Under the assumptions, this is the unique solution when loss aggregation is a linear, unbiased combination.
• Controlled Coefficient of Variation (CV): We can show

Thus, $\Delta L\;Normalization$ guarantees lower CV than DAPO and Dr.GRPO, while matching GRPO at $\alpha=1$. When $\alpha<1$, variance increases slightly, but long responses contribute more effectively.

• Transition to Dr.GRPO: Setting $\alpha=0$ recovers the aggregation method introduced in Dr.GRPO, making it a special case of $\Delta L\;Nomalization$.

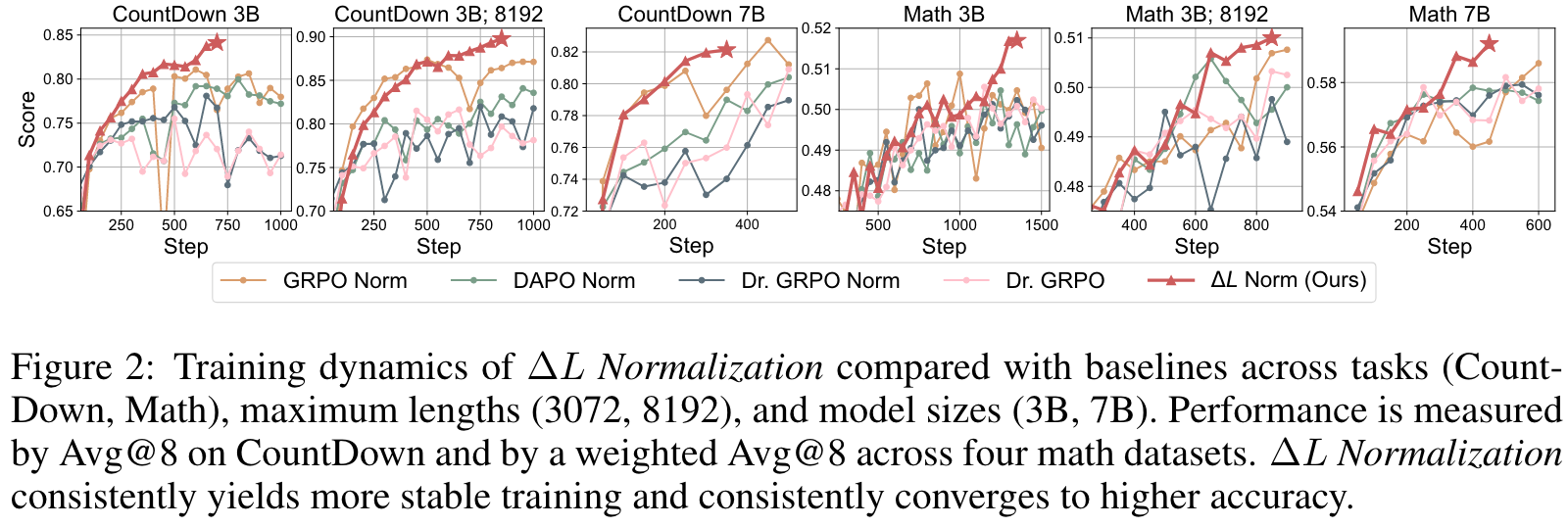
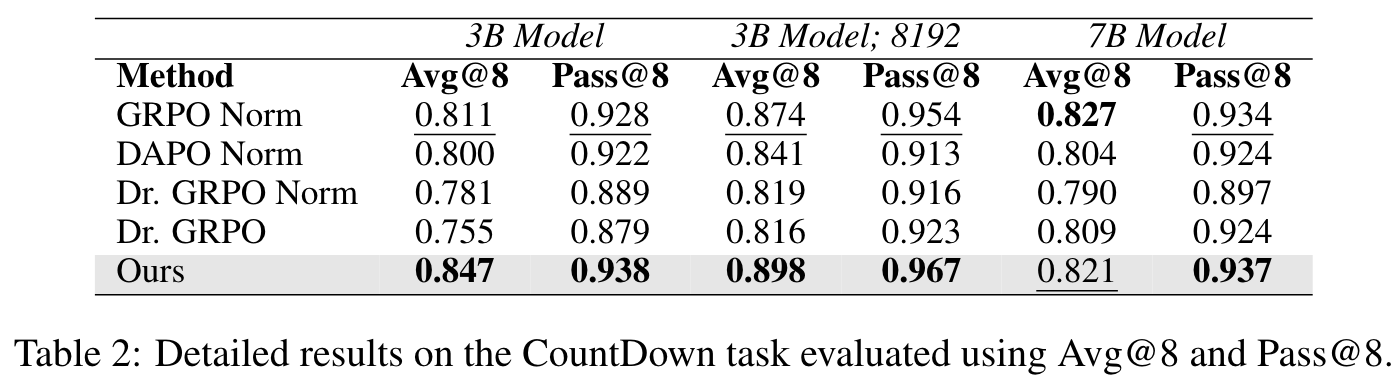
These properties make $\Delta L\;Normalization$ highly valuable for RLVR training. The unbiasedness property ensures consistency with standard reinforcement learning theory, preventing unexpected slowdowns caused by biased gradient estimates. Variance reduction further stabilizes training and accelerates convergence. In practice, we find that, setting $\alpha=1$, which minimizes the variance, is a universal good choice. $\alpha=0.75$ further increase the performance in Math, which might be due to the fact that the long response in Math task should be better utilized.

🤖

Others