目录
Resource Info Paper http://arxiv.org/abs/2505.13417 Code & Data https://github.com/THU-KEG/AdaptThink Public arXiv Date 2025.06.20
Summary Overview
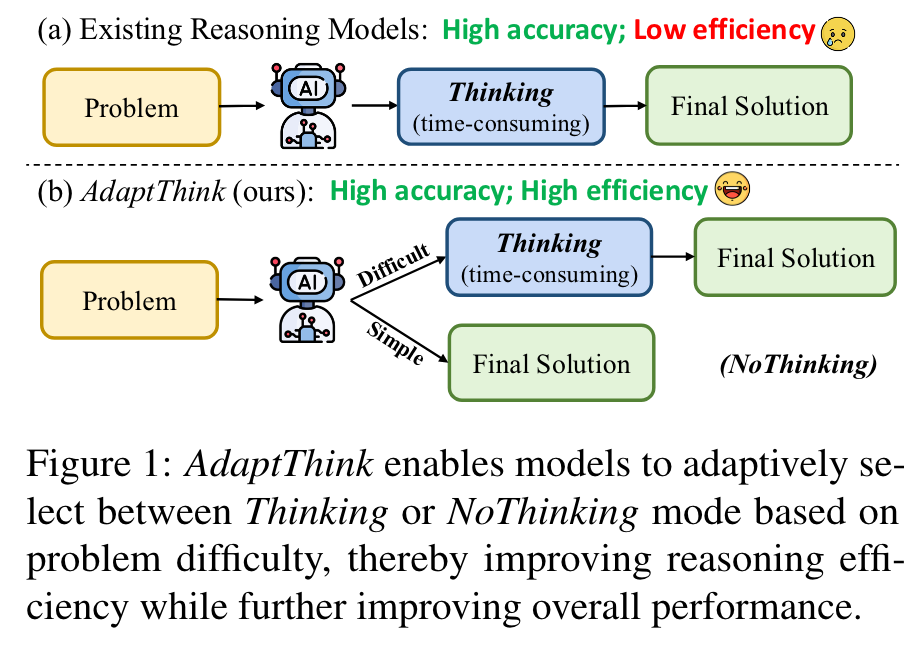
作者认为对于简单的问题,没有必要使用 thinking 模式,而是直接进行回答也能获得很高的准确率。从效率上来说,模型应该有选择的使用 thinking,而不是所有的都开。通过强化学习训练模型,使得模型能够在推理时,自动地选择是否使用 thinking。
AdaptThink, a novel RL algorithm to teach reasoning models to choose the optimal thinking mode adaptively based on problem difficulty.
- a constrained optimization objective that encourages the model to choose NoThinking while maintaining the overall performance;
- an importance sampling strategy that balances Thinking samples during on-policy training, thereby enabling cold start and allowing the model to explore and exploit both thinking modes throughout the training process.
Main Content
Can the reasoning model learn to select Thinking or NoThinking mode adaptively based on the difficulty of the input problem, thereby achieving more efficient reasoning without sacrificing or even improving performance?
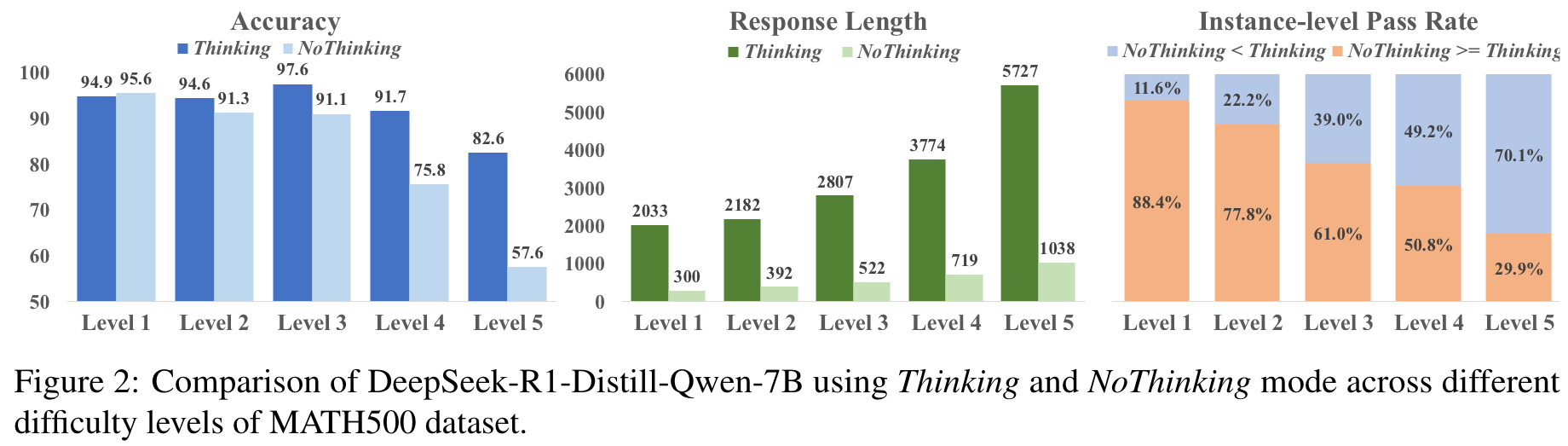
Constrained Optimization Objective
an ideal selection policy should prefer to choose NoThinking as long as the overall performance is not diminished. Let denote the reference model, which is the initial and remains unchanged during training.
To solve this constrained optimization problem, we incorporate the constraint into the objective as a penalty term, with a penalty weight :
By dividing the both side by , letting , and reorganizing the terms about , we have:
In pracitice, can be approximated by pre-sampling before training. Specifically, we sample responses from for each , and calculate their mean reward:
Then the optimization objective becomes:
Since and are not differentiable, we employ policy gradient method to solve this optimization. Specifically, let be a distribution equal to without gradient update, and define the advantage function: . Then the objective can be converted into a PPO-style loss without KL penalty:
To solve cold-start challenge, we employ the technique of importance sampling. Specifically, we define a new distribution :
During training, we sample responses from instead of , so that half of the samples in a batch are in Thinking mode and the other half are NoThinking.

🤖
-
论文的创新之处与独特性:
-
创新之处:
- 适应性思维模式选择:论文提出了AdaptThink,这是一种基于强化学习的算法,能够根据问题难度动态选择“思考模式(Thinking)”或“直接生成模式(NoThinking)”。这种方法显著优化了推理效率,同时在性能上也有所提升。
- 约束优化目标:AdaptThink在优化目标中引入了约束条件,鼓励模型在不降低整体性能的情况下优先选择NoThinking模式。这种方法有效减少了推理成本。
- 重要性采样策略:通过在训练过程中平衡Thinking和NoThinking样本的采样,解决了冷启动问题,并为模型提供了更全面的探索和利用空间。
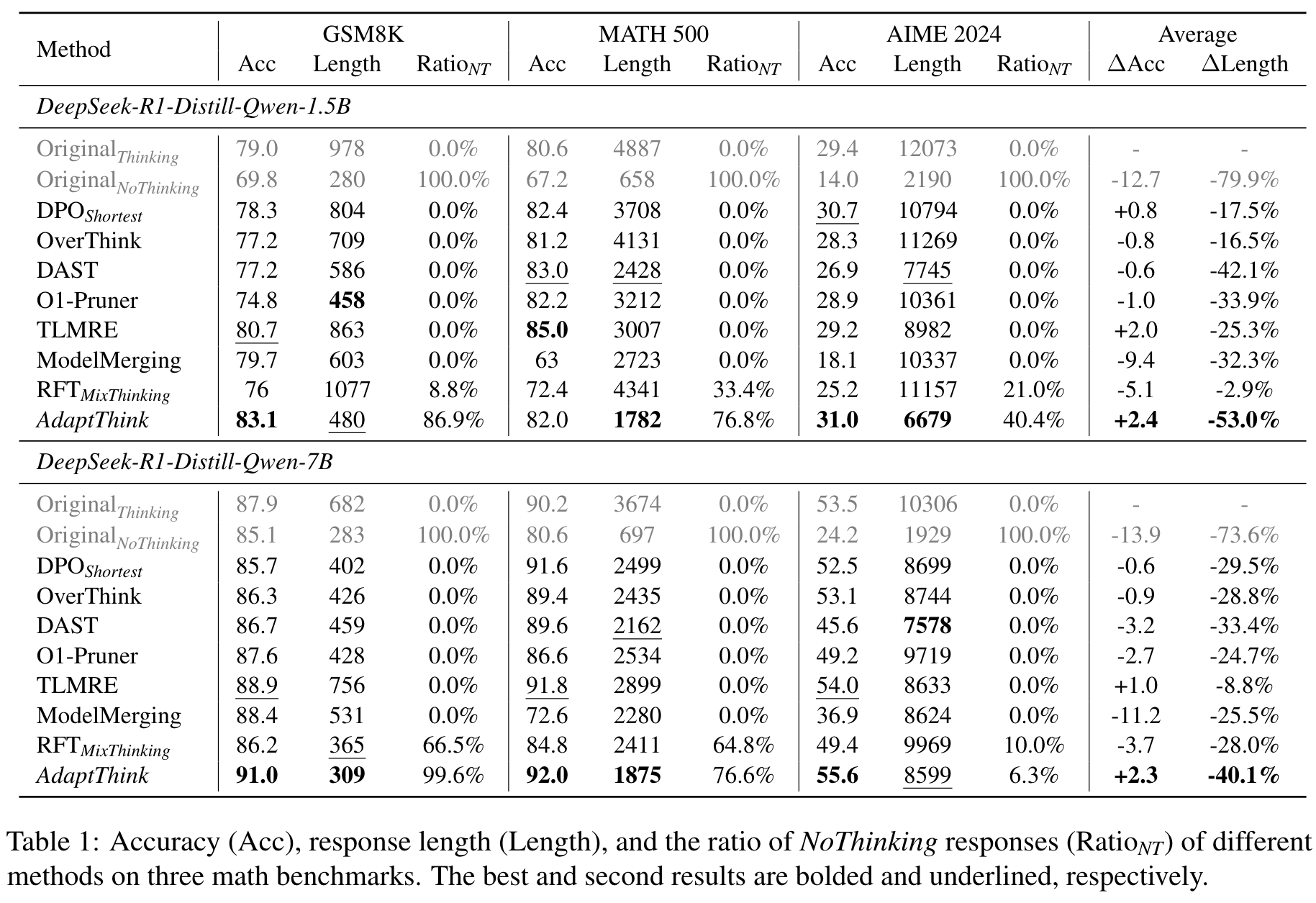
- 显著的实验结果:在多个数学数据集(如GSM8K、MATH500和AIME2024)上的实验表明,AdaptThink不仅减少了推理成本(平均减少53%),还提升了准确率(平均提升2.4%)。
-
独特性:
- 论文首次系统性地研究了思维模式选择与问题难度的关系,明确指出简单问题中NoThinking模式的效率和性能优势。
- 提出的算法不仅适用于数学问题,还在跨领域任务(如MMLU)中展示了良好的泛化能力。
-
关键学习点:
- 在推理任务中,问题难度是决定推理模式的重要因素。
- 通过强化学习和重要性采样,可以在不同推理模式之间实现高效的动态切换。
- 对于简单问题,减少冗余推理步骤有助于显著提升模型效率。
-
-
论文中存在的问题及改进建议:
-
问题1:对复杂问题的处理仍依赖传统Thinking模式
尽管论文提出了NoThinking模式的优势,但在复杂问题中,模型仍然依赖Thinking模式,未能完全优化推理过程。- 改进建议:探索更高效的“简化思维(Simplified Thinking)”模式,即在Thinking模式中通过剪枝或动态调整推理深度来优化复杂问题的推理效率。
-
问题2:适用性验证范围有限
论文的实验主要集中在数学数据集上,尽管在MMLU中展示了一定的泛化能力,但对其他领域(如医疗、法律)的适用性尚未验证。- 改进建议:扩展实验范围,将AdaptThink应用于更多领域的任务,如多模态推理、开放域问答等,以验证其通用性。
-
问题3:NoThinking模式的隐性思维问题
实验中提到,NoThinking模式可能激活隐性思维特征,导致生成的结果仍包含部分冗余推理。- 改进建议:在强化学习训练中引入显式的奖励约束,检测并惩罚隐性思维特征,从而进一步优化NoThinking模式的效率。
-
问题4:对问题难度的量化缺乏细化
论文中对问题难度的定义较为粗略,主要依赖数据集的预定义分类。- 改进建议:设计一种动态的难度评估机制,结合问题的语义复杂度、结构特征和历史解答记录,为每个问题分配更精确的难度评分。
-
-
基于论文的内容和研究结果,提出的创新点或研究路径:
- 创新点1:动态推理深度控制
在Thinking模式中引入动态推理深度控制机制,根据问题难度调整推理链的长度,从而进一步优化复杂问题的推理效率。 - 创新点2:多模态适应性推理
将AdaptThink扩展到多模态任务中(如视觉-语言推理),研究不同模态下思维模式选择的适应性。 - 创新点3:基于用户需求的个性化推理模式选择
结合用户的时间需求和偏好,动态调整推理模式,以实现更好的用户体验。
- 创新点1:动态推理深度控制
-
为新的研究路径制定的研究方案:
-
研究路径1:动态推理深度控制
- 研究方法:
- 在Thinking模式中引入推理深度控制模块,动态监控生成的推理链长度。
- 基于问题的难度评分和当前推理步骤的置信度,动态决定是否继续推理或终止并生成答案。
- 研究步骤:
- 构建包含不同复杂度问题的数据集,并标注每个问题的最优推理链长度。
- 设计强化学习算法,将推理深度作为一个可控变量,优化模型的推理效率和准确率。
- 在数学和常识问答任务上验证方法的有效性。
- 期望研究成果:
- 显著减少复杂问题的推理时间。
- 提高模型在复杂问题上的准确率,同时保持推理链的简洁性。
- 研究方法:
-
研究路径2:多模态适应性推理
- 研究方法:
- 将AdaptThink的思维模式选择机制扩展到多模态任务中,例如视觉-语言推理。
- 在多模态任务中定义不同模态的推理难度,并设计联合优化目标。
- 研究步骤:
- 构建多模态推理数据集(如视觉问答、视频字幕生成)。
- 在多模态Transformer架构中集成AdaptThink算法,研究不同模态下思维模式的选择策略。
- 评估模型在多模态任务中的效率和性能。
- 期望研究成果:
- 提出一种适用于多模态任务的高效推理框架。
- 在视觉-语言推理任务中实现更高的效率和准确率。
- 研究方法:
-
研究路径3:基于用户需求的个性化推理模式选择
- 研究方法:
- 引入用户偏好建模模块,根据用户的时间需求(如快速响应或高质量推理)动态调整推理模式。
- 在强化学习中加入用户偏好奖励函数。
- 研究步骤:
- 收集用户在不同任务中的偏好数据,构建用户需求数据集。
- 设计强化学习算法,结合用户偏好和问题难度,优化推理模式选择。
- 在对话系统和实时问答场景中进行实验验证。
- 期望研究成果:
- 实现基于用户需求的个性化推理,显著提升用户体验。
- 提供一种通用的用户偏好建模方法,可扩展到其他交互式AI任务。
- 研究方法:
-
Others
本文作者:Geaming
本文链接:
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!